Реализовать алгоритм по автоматам на Хаскеле

Question

Мне нужно проверить, допускает ли автомат слово, которое состоит из одинаковых символов. Если хотя бы одно такое есть, то нужно вывести его, если нет - вывести "NO". Для каждого символа из входного алфавита мы запускаем поиск, и если мы пришли в финальный стан, то должны вывести это слово. Если мы дважды попали не в финальный стан, то прекратить поиск для конкретной буквы(попали в цикл). Я написал часть кода, создал тип автомат, но не знаю как реализовать сам алгоритм на haskell.

main = do { 
print(goal m1);
print(goal m2);
print(goal m3);
print(goal m4);
}
w = "abab" 
type FSM q = ([q], Alphabet, [Transition q], q, [q]) 
type Alphabet = [Char] 
type Transition q = (q, Char, q)
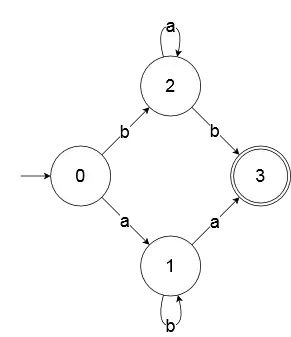
m1 :: FSM Int 
m1 = ([0, 1, 2, 3], 
      ['a', 'b'], 
      [(0, 'a', 1), (1, 'a', 3), (2, 'a', 2), 
       (0, 'b', 2), (2, 'b', 3), (1, 'b', 1)], 
      0, 
      [3] 
    )
m2 :: FSM Int 
m2 = ([0, 1, 2, 3], 
      ['a', 'b'], 
      [(0, 'a', 1), (1, 'a', 3), (2, 'a', 2), 
       (0, 'b', 2), (2, 'b', 3), (1, 'b', 1), 
       (3, 'a', 3), (3, 'b', 3)], 
      0, 
      [3] 
    )
m3 :: FSM Int 
m3 = ([0, 1, 2, 3], 
      ['a', 'b'], 
      [(0, 'a', 1), (1, 'a', 3), (2, 'a', 2), 
       (0, 'b', 2), (2, 'b', 3), (1, 'b', 1), 
       (3, 'a', 1), (3, 'b', 3) ], 
      0, 
      [3] 
    )
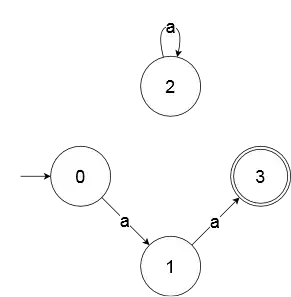
m4 :: FSM Int 
m4 = ([0, 1, 2, 3, 4, 5], 
      ['a', 'b'], 
      [(0, 'a', 1), (1, 'a', 2), (2, 'a', 3), 
       (3, 'a', 5), (5, 'a', 4), (1, 'b', 1), 
       (3, 'b', 1), (3, 'b', 3) ], 
      0, 
      [4] 
    )
states :: FSM q -> [q] 
states (u, _, _, _, _) = u
alph :: FSM q -> Alphabet 
alph (_, a, _, _, _) = a
trans :: FSM q -> [Transition q] 
trans (_, _, t, _, _) = t
start :: FSM q -> q 
start (_, _, _, s, _) = s
final :: FSM q -> [q] 
final (_, _, _, _, f) = f
delta :: FSM Int -> Int -> Char -> Int 
delta m st symbol | length [q1 | (q0, x, q1) <- trans m, q0 == st, x == symbol] > 0 = [q1 | (q0, x, q1) <- trans m, q0 == st, x == symbol] !! 0 | otherwise = -1
goal:: FSM Int -> String
goal m = seek m (alph m) where
    seek m [] = "No"
    seek m (x:xs) | find_letter m x > 0 = create_word x (find_letter m x) [] | otherwise = seek m xs
find_letter:: FSM Int -> Char -> Int 
find_letter m s = dfs m s (start m) [start m] 0 where
    dfs m s state states count 
        | (delta m state s) elem states = 0 
        | (delta m state s) == -1 = 0 
        | (delta m state s) elem (final m) = count + 1
        | otherwise = dfs m s (delta m state s) (states++[delta m state s]) (count+1)
create_word:: Char -> Int -> [Char] -> [Char]
create_word symbol 0 list = list
create_word symbol count list = create_word symbol (count-1) (list++[symbol])

Answer 1

Задача сводится к поиску пути в ориентированном графе. Например, для вашего случая m1

Нужно найти один из путей из начального состояния (четвертое поле типа FSM) – вершины 0 на диаграмме, до одного из заключительных состояний (пятое поле типа FSM), в данном случае оно одно – это вершина 3. При этом использовать только одинаково промаркированные ребра, например, только a или только b.

Т.е. алгоритм будет таким

• Берем один из символов алфавита, например, a
• Удаляем все ребра, промаркированные другими символами.
• Ищем путь от вершины 0 до вершины 3 (например, поиском в ширину)

В данном случае это будет путь 0→1→3 через два ребра a, значит автомат допускает как минимум одну подходящую строку – aa

Если путь не найден, повторяем действия для других заключительных состояний и оставшихся символов.

---

Дополнение после правок в вопросе

Если не менять ваш алгоритм, получится примерно так

import Data.Maybe (fromMaybe, listToMaybe)
import Data.Foldable (asum)
...
delta :: Eq a => FSM a -> a -> Char -> Maybe a
delta m st symbol = listToMaybe [q1 | (q0, x, q1) <- trans m, q0 == st, x == symbol]
goal :: Eq a => FSM a -> String
goal m = fromMaybe "No" $ asum [flip replicate x <$> find_letter m x | x <- alph m]
find_letter :: Eq a => FSM a -> Char -> Maybe Int
find_letter m s =  dfs (start m) [start m] 1
  where
    dfs state seen count =
      case delta m state s of
        Nothing -> Nothing
        Just nextState
          | nextState elem seen -> Nothing
          | nextState elem final m -> Just count
          | otherwise -> dfs nextState (nextState : seen) (count + 1)

Но имейте в виду, что в изначальном вопросе у вас был один недетерминированный автомат m4, и с ним, по понятной причине алгоритм не сработает.

От себя могу предложить такой вариант: Так как минимальное количество символов в допустимом слове у вас не может превысить количество состояний, можно просто скармливать автомату по одной букве, пока не достигнем заключительного состояния или пока не превысим количество узлов.

Вот пример для недетерминированного автомата.

m4 :: FSM Int
m4 = ([0,1,2,3,4,5,6,7],
      ['a', 'b'],
      [(0,'a',1), (1,'b',1), (1,'a',4), (0,'a',3),
      (0,'b',2), (3,'b',2), (2,'b',5), (5,'a',5),
      (4,'b',6), (5,'a',6), (6,'b',3), (3,'a',5),
      (6,'a',7), (7,'b',7), (7,'a',4)],
      0,
      [7])
next :: Eq a => FSM a -> Char -> a -> [a]
next m char st = [to | (from, x, to) <- trans m, x == char, st == from]

GHCi> take (length (states m4)) $ iterate (nub . (>>= next m4 'a')) [start m4]
[[0],[1,3],[4,5],[5,6],[5,6,7],[5,6,7,4],[5,6,7,4],[5,6,7,4]]
GHCi> take (length (states m4)) $ iterate (nub . (>>= next m4 'b')) [start m4]
[[0],[2],[5],[],[],[],[],[]]

Для буквы a заключительное состояние 7 достигается на пятом шаге, значит в слове 4 буквы a. Для буквы b заключительное состояние не достигается.