Золотое сечение МО

Question

#include <iostream>
#include <math.h>
#include <conio.h>
#include <iomanip>

using namespace std;

double func(double x) // функция вызова функции
{
    return  (10*x*log10(x)/log10(2.7)-(x*x)/2); // заданная задачей функция 
}



void mZolotSech(int N, double a,double b) // сам метод
{
    long double x1,x2,y1,y2, ymin, xmin,t, er,ea; // er -> расчетная погрешность, еа->вычисляемая погрешность.
    int m,j;
    t=(1+sqrtl(5))/2; // то самое phi, отношение золотого сечения
    er=(b-a)/(2*pow(t, (N-1))); 
    x1=b-(b-a)/t;   y1=func(x1);
    x2=a+(b-a)/t;   y2=func(x2);
    m=2;
    do
    {   
        if(y1<y2)
           {b=x2;
            x2=x1; y2=y1;
            x1=b-(b-a)/t;
            y1=func(x1);
            cout<<"m="<<m<<" x1="<<x1<<" x2="<<x2<<" y1="<<y1<<" y2="<<y2<<endl;
            }
            else
            { a=x1;
            x1=x2; y1=y2;
            x2=a+(b-a)/t;
            y2=func(x2);
            cout<<"m="<<m<<" x1="<<x1<<" x2="<<x2<<" y1="<<y1<<" y2="<<y2<<endl;
            }
            m++;
    }
    while(m<N);
        if(y1<y2) b=x2;
        else a=x1;
        cout<<endl;
        cout<<a<<b;
            xmin=(a+b)/2.0; ymin=func(xmin); ea=(b-a)/2.0;
            cout<<endl;
    cout<<setw(15)<<xmin<<setw(15)<<ymin<<setw(15)<<er<<setw(15)<<ea<<endl;

    _getch();
}


int main()
{
    setlocale(LC_ALL, "Russian");
    cout<<"Добро Пожаловать в программу\n";
    int N; double a,b;
    cout<<"Введите количество экспериментов=";cin>>N;cout<<"\nВведите a=";cin>>a;cout<<"\nВведите b=";cin>>b;
    mZolotSech(N,a,b); 

}

Вот скриншот выполнения программы:

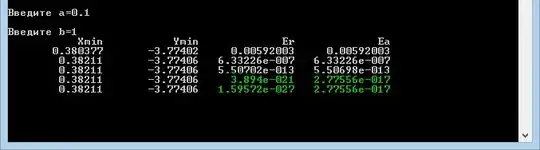
введите сюда описание изображения

Видим 5 строк каждая соответствует: 10,20,30,40,50 итераций. Последние 2 строки отличаются, значительно чего не должно быть.

Описание принципа метода (только при заданном Е (погрешность))

Мой случай: 10х*ln(x)-x*x/2 ограничения: [0.1;1] Задано количество итерация(подсчетов), нужно найти Хmin, Ymin, Ер, Ев. Ер-расчетная погрешность, Ев-вычислительная.

@Adrug игра в Угадайку продолжается? А в "золотом сечении МО" МО -- это министерство обороны? — alexlz, Oct 21 '13 at 17:16
Отредактировал, постарался более глубже передать свою проблему. Мне была поставлена задача: имеющуюся функцию(с границами a,b) пропустить через метод золотого сечения. — Adrug, Oct 21 '13 at 17:25
Ок, про бред своему преподавателю расскажешь ;-) — Утка Учится Укрываться, Oct 21 '13 at 17:28
@Adrug попробуйте считать добавляемые точки (x1 или x2) более традиционным способом (1) Замените sqrtf на sqrt или sqrtl -- зачем там float (2) Ну и исправьте void main на int main — alexlz, Oct 21 '13 at 18:54
@Adrug, вот опубликовали ссылку и стало понятно о чем речь. А в следующий раз излагайте суть задачи сразу (и лучше своими словами, не напрягайте никого лазаньем по ссылкам).
Вы просто неправильно запрограммировали шаг 2 алгоритма по Вашей ссылке. Там же на каждой итерации надо пересчитывать x1 и x2 по скорректированным a и b.

Посмотрите еще раз внимательно на алгоритм и Вашу программу (код в цикле do { ... } while();) — avp, Oct 21 '13 at 19:45
Долго думал на этим куском программы, так и не увидел расхождений. Я обновляю a и b, в конструкции If после каждого прохода цикла. @alexlz ваш совет 1) нормализовал Ер и Еа при итераций = 30, но к сожалению 40 и 50 итераций также расходятся. — Adrug, Oct 23 '13 at 17:07
@avp, может вас смутило, что алгоритм для заданной точности, а мне необходимо найти эту самую точность при заданных итераций. — Adrug, Oct 23 '13 at 17:16
@Adrug Откорректируйте код в вопросе и приведите исходные данные. — alexlz, Oct 23 '13 at 18:17
@Adrug, смотрите , алгоритм по Вашей ссылке
for(;;) { x1 = b-(b-a)/phi; x2 = a+(b-a)/phi; y1 = func(x1); y2 = func(x2); if (y1 >= y2) a = x1; else b = x2; if (abs(b - a) < eps) { x = (a + b) / 2; break; } }

где phi это пресловутое золотое сечение == 1.618... (с eps, надеюсь, все понятно).

А у Вас какой-то совсем не тот алгоритм. Может он и правильный, но причем здесь тогда эта ссылка? — avp, Oct 23 '13 at 19:07
@avp, алгоритм в приведенной ссылке считает количество итераций при заданном Ев(вычислительная погрешность), мне необходимо же найти эту погрешность уже при заданных итераций. @alexlz, привел в код в текущее состояние. Спасибо за понимание. Жду вашей помощи. Расчет был на то что на данном сервисе найдутся люди, которые сталкивались с темой "одномерные методы оптимизации". — Adrug, Oct 24 '13 at 10:59
@Adrug я в преф не играл никогда, но их выражение "канделябрами бить" слышал. Скриншот от какой программы Вы привели? Ну да ладно. Заметил расхождение (1.13061e-19 vs 2.77556e-17) при N=90. Поменял все описания double на long double и log10 на log10l. Результат стал 1.13061e-19 vs 1.21973e-19. Дальше с погрешностями разбирайтесь сами.
И, кстати, из сонсольного (cmd.exe) окна лучше делать copy с последующим paste в текст вопроса, чем лепить скриншот. — alexlz, Oct 24 '13 at 12:56
Мда, судя по количеству минусующих про методы оптимизации здесь мало кто слышал.
Так вот, очевидно что иррациональное число фи комп точно посчитать не может, считает он его с некоторой погрешностью. И эта погрешность накладывает ограничения на точность самого метода, читай в любой методичке по численным методам, например тут: http://www.machinelearning.ru/

Ну и вообще по логике вещей: у тебя порядок длины отрезка который ты хочешь получить -17, а выражения с помощью которых ты этот отрезок ищещь считаются с точностью скажем -10. Ничего странного не видишь? — Утка Учится Укрываться, Oct 24 '13 at 18:14
@Megavolt, методы оптимизации и проблемы погрешности к минусам за ответ отношения (IMHO) не имеют.
В правилах ХК объясняется, что если ответ нравится, то +, а если нет - то -.

Видимо такой ответ не понравился, может его надо было как комментарий написать? — avp, Oct 24 '13 at 18:43
Хз как вам,но здесь http://orenstudent.ru/GoldCutting.htm более доступно описан данный метод — horpion, Oct 02 '14 at 14:25

score 1 · Accepted Answer · edited Apr 13 '17 at 12:53

1

Раз уж вопрос всплыл в очереди проверки:

Точность long double - около 15-17 десятичных цифр. Это означает, что при работе с числами, близкими к 1, вычислителная погрешность будет порядка 10^-17, что и наблюдается в этом примере. Точность 10^-24 требует замены double на что-нибудь более точное.

edited Apr 13 '17 at 12:53

Дух сообщества

1

answered Dec 19 '15 at 12:02

Для меня этот вопрос уже не актуален, думаю вы правы. Спасибо что помогли! – Adrug Dec 21 '15 at 14:13

Золотое сечение МО

1 Answers1