Алгоритм поиска минимального набора различимых групп в таблице

Question

Речь идет о прикладной задаче: словаре неисправностей (в качестве осей там значатся частота и номер неисправности).

Таблица выглядит так (см вложения).

Мне необходимо оптимизировать число частот таким образом, чтобы найти минимальное количество частот, которое уникально идентифицирует каждую неисправность.

При этом в отдельные группы выделяются неисправности(строки), которые совпадают друг с другом (они считаются неразличимыми и не учитываются в общем алгоритме). Быть может кто-то подскажет, какой алгоритм можно для этого использовать или у кого-то есть на примете что-то готовое?

PS - один из примеров решений - для данного словаря - это три частоты (столбцы затенены). Ссылка на статью, в которой я разбираю данную проблематику - https://bib.irb.hr/datoteka/11551.ICECS96.pdf Статья на английском, раздел 3.3 занимается вопросом оптимизации.

Answer 1

Если я правильно понял терминологию задачи, требуется найти минимальную комбинацию столбцов для которой строки будут уникальными. (Неразличимые строки можно исключить на этапе предобработки.)

Посмотрите алгоритмы для поиска «minumal unique column combination». Похоже, они делают именно то, что вам нужно.

Heise A. et al. Scalable Discovery of Unique Column Combinations — Описание Ducc, одного из таких алгоритмов.

Abedjan Z., Naumann F. Advancing the Discovery of Unique Column Combinations — Описание алгоритма HCA

Answer 2

Будем накапливать варианты таким образом:

Идем по списку ошибок, считая что у нас есть не более i ошибок. Смотрим какие столбцы определяют однозначно ошибку.

Например, если у нас есть одна (#0) ошибка, ее определить можно по любому столбцу. Заносим в список вариантов решения массивы из одного элемента по каждому столбцу: [[47],[50],[52],...[71]].

Переходим ко второй ошибке (#1), также все столбцы могут определить вторую ошибку, т.к. значения частот для второй ошибки отличаются от значения частот для первой ошибки. Список вариантов остается тем же.

На третей итерации, нас не удовлетворяет 58 столбец, т.к. там идет повтор пятерки. Для 58-го столбца нам понадобится еще один столбец, в данном случае любой. Заменяем [58] на пары, в итоге получаем: [[47],[50],[52],[47,58],...[58,71],...[71]].

Ну и продолжая таким образом делать проверки и при необходимости заменять варианты на комбинации с другими подходящими столбцами мы получим все возможные комбинации столбцов.

Также возможна ситуация, когда добавление одного столбца может быть недостаточно и придется пытаться добавлять два и более. В частности такая ситуация возникнет для ошибок, которые нельзя идентифицировать по имеющимся значениям (#10,#11 и т.д.) - логично исключить эти ошибки заранее.

Оптимальными наборами столбцов окажутся естественно те, длина которых меньше. Вот если бы было только первых пять ошибок, достаточно было бы одного из столбцов 52,53,54,67 или 71. Для шести первых ошибок уже одного столбца было бы недостаточно, были бы пары...

Иллюстрация предложенного алгоритма:

function go(maxColumnsCount) {
  var results = [];
  for (var er = 0; er < errors.length; er++) {
    if (!results.length) {
      // первоначальное заполнение
      for (var c = 0; c < colcount; c++) {
        results.push([c]);
      }
    } else {
      var newResults = [];
      for (var r = 0; r < results.length; r++) {
        // проверяем существующие кандидаты на валидность для следующей ошибки
        if (isUnique(results[r], newResults) && checkCollisions(results[r], er)) {
          newResults.push(results[r]);
        } else {
          for (var i = 0; i < colcount; i++) {
            var candidateresult = results[r].slice();
            if (candidateresult.length < maxColumnsCount && candidateresult.indexOf(i) < 0) {
              candidateresult.push(i);
              if (isUnique(candidateresult, newResults) && checkCollisions(candidateresult, er)) {
                newResults.push(candidateresult);
          }

        }
      }
    }
  }
  if (newResults.length) {
    results = newResults;
  } else {
    logIt("error cannot be indentified [" + er + "]:" + errors[er]["name"]);
  }
}
//logIt(JSON.stringify(results));

}
  logIt(JSON.stringify(results));
}
function checkCollisions(res, row) {
  var values = [];
  for (var r = 0; r < res.length; r++) {
    values.push(errors[row]["f"][res[r]]);
  }
  for (var cr = 0; cr < row; cr++) {
    var same = true;
    for (var v = 0; v < values.length; v++) {
      if (values[v] != errors[cr]["f"][res[v]]) {
        same = false;
        break;
      }
    }
    if (same) return false;
  }
  return true;
}
function isUnique(candidate, results) {
  candidate.sort(function(a, b) {
    return a - b
  });
  for (var r = 0; r < results.length; r++) {
    if (candidate.length == results[r].length) {
      var same = true;
      for (var c = 0; c < candidate.length; c++) {
        if (candidate[c] != results[r][c]) {
          same = false;
          break;
        }
      }
      if (same) {
        return false;
      }
    }
  }
  return true;
}
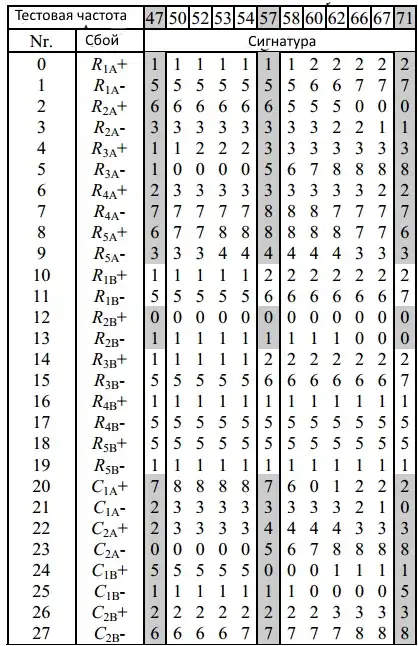
var errors = [{
  "name": "R1A+",
  "f": [1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2]
}, {
  "name": "R1A-",
  "f": [5, 5, 5, 5, 5, 5, 5, 6, 6, 7, 7, 7]
}, {
  "name": "R2A+",
  "f": [6, 6, 6, 6, 6, 6, 5, 5, 5, 0, 0, 0]
}, {
  "name": "R2A-",
  "f": [3, 3, 3, 3, 3, 3, 3, 3, 2, 2, 1, 1]
}, {
  "name": "R3A+",
  "f": [1, 1, 2, 2, 2, 3, 3, 3, 3, 3, 3, 3]
}, {
  "name": "R3A-",
  "f": [1, 0, 0, 0, 0, 5, 6, 7, 8, 8, 8, 8]
}, {
  "name": "R4A+",
  "f": [2, 3, 3, 3, 3, 3, 3, 3, 3, 3, 2, 2]
}, {
  "name": "R4A-",
  "f": [7, 7, 7, 7, 7, 8, 8, 8, 7, 7, 7, 7]
}, {
  "name": "R5A+",
  "f": [6, 7, 7, 8, 8, 8, 8, 8, 8, 7, 7, 6]
}, {
  "name": "R5A-",
  "f": [3, 3, 3, 4, 4, 4, 4, 4, 4, 3, 3, 3]
}, {
  "name": "R1B+",
  "f": [1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2]
}, {
  "name": "R1B-",
  "f": [5, 5, 5, 5, 5, 6, 6, 6, 6, 6, 6, 7]
}, {
  "name": "R2B+",
  "f": [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
}, {
  "name": "R2B-",
  "f": [1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0]
}, {
  "name": "R3B+",
  "f": [1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2]
}, {
  "name": "R3B-",
  "f": [5, 5, 5, 5, 5, 6, 6, 6, 6, 6, 6, 7]
}, {
  "name": "R4B+",
  "f": [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1]
}, {
  "name": "R4B-",
  "f": [5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5]
}, {
  "name": "R5B+",
  "f": [5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5]
}, {
  "name": "R5B-",
  "f": [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1]
}, {
  "name": "C1A+",
  "f": [7, 8, 8, 8, 8, 7, 6, 0, 1, 2, 2, 2]
}, {
  "name": "C1A-",
  "f": [2, 3, 3, 3, 3, 3, 3, 3, 3, 2, 1, 0]
}, {
  "name": "C2A+",
  "f": [2, 3, 3, 3, 3, 4, 4, 4, 4, 3, 3, 3]
}, {
  "name": "C2A-",
  "f": [0, 0, 0, 0, 0, 5, 6, 7, 8, 8, 8, 8]
}, {
  "name": "C1B+",
  "f": [5, 5, 5, 5, 5, 0, 0, 0, 1, 1, 1, 1]
}, {
  "name": "C1B-",
  "f": [1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 5]
}, {
  "name": "C2B+",
  "f": [2, 2, 2, 2, 2, 2, 2, 2, 3, 3, 3, 3]
}, {
  "name": "C2B-",
  "f": [6, 6, 6, 6, 7, 7, 7, 7, 7, 8, 8, 8]
}];
var colcount = errors[0]["f"].length;
document.getElementById("go").addEventListener("click", function() {
  go(parseInt(document.getElementById("maxCol").value) || 3);
});
document.getElementById("clear").addEventListener("click", function() {
  document.getElementById("log").value = "";
});
function logIt(msg) {
  var memo = document.getElementById("log");
  memo.value = memo.value + "\n" + msg;
}

html,
body {
  height: 100%;
  margin: 0;
  padding: 0
}
#log {
  height: 100%;
  width: 100%;
  border: 0;
  padding: 0
}
#maxCol {
  position: absolute;
  top: 10px;
  right: 100px;
}
#go {
  position: absolute;
  top: 10px;
  right: 50px
}
#clear {
  position: absolute;
  top: 30px;
  right: 50px
}

<textarea id="log"></textarea>
<input type="text" id="maxCol" value="3" placeholder="Максимальное количество колонок">
<button id="go">go</button>
<button id="clear">clear log</button>

По поводу оптимизации. Добавлено искусственное ограничение на количество столбцов в варианте, это для дебага. Надо уметь отсекать наборы, которые целиком включают более короткие наборы колонок.

Answer 3

Первое, что пришло в голову -- попробуйте такую идею.

Сначала выбросим все строки, которые однозначно не идентифицируются всем набором столбцов.

Для оствшихся.

Для каждого столбца i найдем A[i] -- количество разных значений. Рассортируем столбцы по убыванию A[i].

Строим решение, начиная с первого в порядке нашей сортировки столбца, добавляя столбцы, пока все строки не будут однозначно идентифицированы.

На самом деле, скорее всего это не оптимальное решение (доказать его оптимальность даже не буду пытаться), но сходу придумать опровергающий пример не получилось.

В любом случае, если дальше (после первого шага) пробовать какой-то перебор, то видимо надо в первую очередь добавлять столбцы которые однозначно идентифицируют максимальное число строк.

Answer 4

Можно разбить сигнатуры на группы по повторам в выбранном первом разряде и перебрать возможные варианты разрядов делающие сигнатуры уникальными.

• Убираем общие и уникальные сигнатуры. Остались только сигнатуры с повторами.
• Выбираем разряд(столбец) сигнатуры, который охватывает максимум комбинаций(назову его S1) и добавляем в список используемых разрядов. Для этого считаем повторы значений сигнатуры для каждой частоты.
• Группируем сигнатуры с одинаковыми значениями в разряде S1. Для их идентификации требуется больше разрядов.

• Для каждой группы сигнатур определяем разряды(1 или более) делающие их уникальными:

  • Перебираем неиспользуемые разряды.
  • Проверяем делает ли текущий разряд вместе с используемыми все сигнатуры в группе уникальными.
  • Если делает, то добавляем его в список используемых разрядов.
  • Если ни 1 разряд не делает все сигнатуры уникальными, то выбираем тот который делает большинство сигнатур в группе уникальными и добавляем его в список используемых разрядов, и создаём новую группу с неразрешёнными в текущей группе сигнатурами.

Сделав все группы сигнатур уникальными мы минимизировали кол-во используемых разрядов, т.е нашли минимальное количество частот, которое уникально идентифицирует каждую неисправность.

Может быть ситуация в которой для воссоздания уникальности всех сигнатур в группе будет достаточно выбрать разряд, например, S3 или S7, но неизвестно какой из них будет лучше для других групп сигнатур. Можно или взять любой из них, что будет быстро, либо проверить этот разряд для других групп, что будет медленно, но может дать лучший результат.