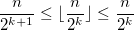Алгоритмы. Сколько раз вызывается print() в функции? Временная сложность циклов с половинным делением i /= 2

Question

Сколько раз вызывается print() в зависимости от параметра n?

def f5(n):
    i = n
    while i > 0:
        j = i
        while j > 0:
            print(i, j)
            j = j - 1
        i = i // 2

def f6(n):
    i = n
    while i > 0:
        j = i
        while j > 0:
            print(i, j)
            j = j // 2
        i = i - 1

Answer 1

Ну, понятно, что это

и

но как это записывается в аналитическом виде - Кнут его знает :) По крайней мере в Конкретной математике для первой формулы даны только оценки в разделе 4.4, и пояснено, что эту сумму очень легко считать в бинарном виде, отбрасывая по одному младшему биту...

Update На незаданный вопрос о временной сложности, естественно, не отвечал. Но если автора действительно интересует ответ и на этот вопрос, то

Первое определяется с учетом того, что реальное значение

так что оценку сделать легко и сверху, и снизу. Аналогичная оценка выполняется и для второго случая с учетом формулы Стирлинга

Answer 2

Если T(n) = T(n-1) + c, где T(n)—это количество шагов, выполняемых циклом при заданном n, то T(n) = O(n). Если T(n) = T(n/2) + c, то T(n) = O(log(n)).

В первом случае внутренний цикл повторяется: n + n/2 + n/4 + n/8 + ... ~ n, учитывая что:

То есть f5(n)—это O(n) алгоритм, не смотря на то что на первый взгляд код в f5() может выглядеть как O(n log n) алгоритм.

С другой стороны, точное значение можно легко найти, используя Питон, просто заменив print() в коде вопроса на count += 1 и заметив, что вложенный цикл выполняется i раз, что позволяет заменить его на count += i:

def count_f5(n):
    count = 0
    if n >= 0:
        i = n
        #  abcde
        # + abcd
        # +  abc
        # +   ab
        # +    a
        while i: # log(n) iterations
            count += i
            i >>= 1  # i //= 2
    return count

---

Во втором случае: log(n) + log(n-1) + log(n-2) ... ~ log(n!) раз:

То есть f6(n)—это O(log(n!)) == O(n log n) алгоритм.

Чтобы получить точное количество print() вызовов в f6(), достаточно заметить, что каждый j //= 2 во вложенном цикле отбрасывает одну цифру в двоичном представлении j, поэтому общее количество итерацией во вложенном цикле равно количеству цифр в двоичном представлении i, то есть i.bit_length() на Питоне, метод который возвращает количество бит в числе.

Тогда точное число print() вызовов в f6() можно найти, используя прямолинейный цикл по i:

def count_f6_bruteforce(n):
    return sum(i.bit_length() for i in range(1, n+1))

Этот код можно упростить и свести к явной формуле:

def count_f6(n):
    if n < 1:
        return 0
    # 2**(nbits - 1) <= n < 2**nbits
    nbits = n.bit_length()
    return nbits * (n + 1) - 2**nbits + 1