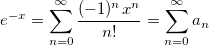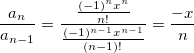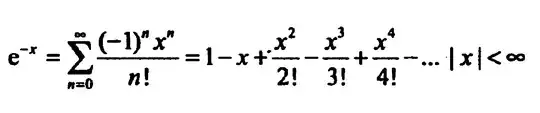Оптимизация программы. Деление на факториал. Ряд Тейлора

Question

Есть функция, которая вычисляет значение математической функции путем разложения в ряд Тейлора. Преподаватель из университета сказал, что лучше не делить на факториал, а сделать как то по другому. Как можно оптимизировать данную функцию, что бы убрать факториал из знаменателя?

double function(const double x)
{

    int n=0,i;
    long long int factor;
    double eps=0.0001,F=eps+1.0, Sum=0;
    while(eps <= F)//Если модуль значения функции меньше чем eps, прекращаем суммирование
    {
        for(i=2,factor=1;i<=n;i++)
            factor*=i;
        F=(pow(-1,n) * pow(x,n)) / factor;
        Sum+=F;
        if(F<0)//Узнаем модуль "F", для сравнивания с "eps" ибо значение может быть отрицательным.
            F*=-1;
        n++;
    }
    return Sum;
}

Answer 1

Нет необходимости вычислять факториал. Можно использовать рекуррентное соотношение.

Ниже приведена демонстрационная программа, в которой для сравнения результатов используется стандартная C-функция exp, объявленная в заголовке <math.h>. Естественно, для работы написанной функции эта стандартная функция и соответствующий заголовок не нужны.

#include <stdio.h>
#include <float.h>
#include <math.h>

double f(double x)
{
    double sum = 1.0;
    double member = 1.0;

    for ( int n = 1; !(fabs( member ) < DBL_EPSILON); n++ )
    {
        member = member * -x / n;
        sum += member;
    }

    return sum;
}

int main( void )
{
    for (int i = 1; i < 10; i++)
    {
        printf( "%lf %lf\n", f(i ), exp(-i));
    }
}

Вывод программы на консоль:

0.367879 0.367879
0.135335 0.135335
0.049787 0.049787
0.018316 0.018316
0.006738 0.006738
0.002479 0.002479
0.000912 0.000912
0.000335 0.000335
0.000123 0.000123

Как видно из вывода результаты для показанной функции и стандартной C функции exp совпадают.

Answer 2

Вероятнее всего преподаватель имел ввиду то, что очередной член ряда для заданной функции можно вычислить рекуррентно.

Выпишите члены ряда:

a_{0} = 1
a_{1} = - x/1
a_{2} = x^2/(1*2)
a_{3} = -x^3/(1*2*3)
a_{4} = x^4/(1*2*3*4)

Отсюда видно, что i-й член ряда можно вычислить исходя из i-1-го члена и значения i:

a_{i} = a_{i-1}*(-x/i), при i = 1,2...

При таком подходе внутренний цикл можно убрать.

Answer 3

Чтоб было понятнее, распишу математику подробнее:

Ну, или еще подробнее :) -

Так что в результате ряд считается простой функцией

double exp_neg(double x, double eps)
{
    double sum = 1.0, term = 1.0;
    for(int n = 1; term > eps || term < -eps; ++n)
    {
        sum += term *= -x/n;
    }
    return sum;
}

Кстати, тут яркий пример случая, когда не нужно применять pow.