Количество точек с целыми координатами в пересечении окружностей

Question

Есть две окружности, заданные 2я координатами и радиусом - (x1, y1, r1), (x2, y2, r2).

Необходимо найти количество точек с целыми координатами, которые находятся одновременно в двух окружностях. Все значения по модулю не превосходят 10⁶.

UPD: Вот моя попытка:

x1, y1, r1 = map(int, input().split(' '))
x2, y2, r2 = map(int, input().split(' '))

size_x_min = min([x1-r1, x2-r2])
size_x_max = max([x1+r1, x2+r2])
size_y_min = min([y1-r1, y2-r2])
size_y_max = max([y1+r1, y2+r2])

r1 = r1**2
r2 = r2**2

count = 0

for y in range(size_y_min, size_y_max):
    for x in range(size_x_min, size_x_max):
        if (x1 - x)**2 + (y1 - y)**2 <= r1 and (x2 - x)**2 + (y2 - y)**2 <= r2:
            count += 1
print(count)

Но код выполняется слишком медленно.

Пример:
окр 1 - (0, 0, 5)
окр 2 - (2, 2, 3)
Точек (ответ) - 26

Answer 1

Но код выполняется слишком медленно

Ваш алгоритм квадратичный по радиусу. Использование меньшего из двух радиусов этого не изменит. В худшем случае один круг в другом лежит, поэтому количество точек в пересечении равно количеству точек в меньшем круге. Количество точек, лежащих на координатной решётке, внутри круга пропорционально площади круга, то есть ~r². Поэтому любой метод, в котором точки по одной считаются, будет квадратичным, то есть ведёт к ~10¹² операций в этом случае (медленно).

Можно использовать линейный алгоритм, чтобы улучшить эффективность для больших радиусов. В конце ответа по ссылке подробное объяснение почему квадратичный алгоритм гораздо хуже линейного (для больших радиусов).

Чтобы получить линейный алгоритм, можно обходить только одну координату (к примеру, вертикально по y), а количество точек (горизонтальных) в пересечении вычислять сразу, определяя пересечение интервалов, ограниченных заданными окружностями:

from math import ceil, floor

def count_lattice_points_intersection(a, b):
    count = 0
    for y in range(a.y - a.r, a.y + a.r + 1):  # scan from bottom to top
        if b.y - b.r <= y <= b.y + b.r:  # intersection is possible
            # find intersection boundaries for given y
            ax1, ax2 = x_coordinates_intesect(a, y)
            bx1, bx2 = x_coordinates_intesect(b, y)
            if min(ax2, bx2) >= max(ax1, bx1):  # intersect
                count += floor(min(ax2, bx2)) - ceil(max(ax1, bx1)) + 1
    return count

def x_coordinates_intesect(c, y):
    """Get x-coordinates of intersection of circle *c* and horizontal line *y*."""
    # solve quadratic equation
    # (x - c.x)**2 + (y - c.y)**2 == c.r**2
    assert c.r**2 >= (y - c.y)**2
    D = (c.r**2 - (y - c.y)**2)**.5
    return c.x - D, c.x + D

Границы интервалов находятся решив квадратное уравнение для окружности:

(x - c.x)**2 + (y - c.y)**2 == c.r**2

Пример:

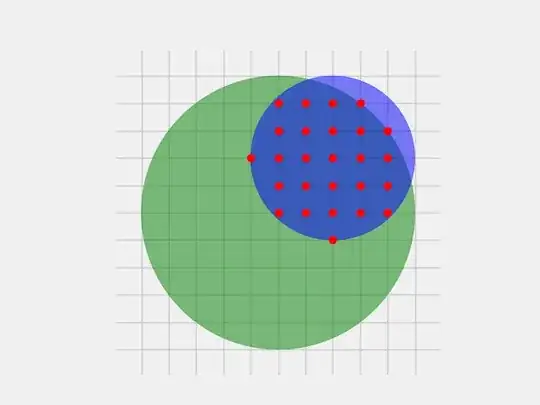
from collections import namedtuple

Circle = namedtuple('Circle', 'x, y, r')
print(count_lattice_points_intersection(Circle(0, 0, 5), Circle(2, 2, 3)))
# -> 26

26 точек координатной решётки находятся внутри заданных кругов.

Answer 2

Вы перебираете точки квадрата, содержащего обе окружности. Это правильное решение, но таких точек слишком много. В качестве начального квадрата достаточно взять квадрат, в который вписана меньшая окружность (точнее, надо говорить о кругах, а не окружностях).