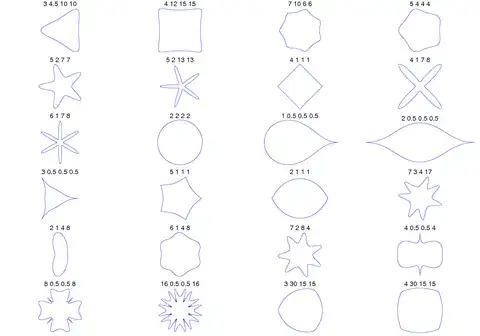
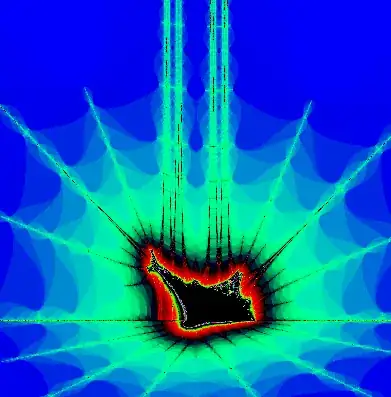
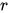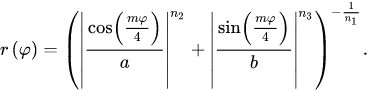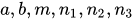Я интересуюсь компьютерной графикой и хотел бы провести своего рода конкурс.
Я хотел бы узнать о новых (для себя) способах генерации различных фракталов или других изображений, полученных по достаточно простой формуле.
То есть критерием соревнования является, - использование простой базовой формулы для получения интересных картинок.
Например есть такая реализация цикла по всем пикселям на картинке:
let c = canvas.getContext('2d'), w = canvas.width, h = canvas.height
let formula = (x, y, cx, cy, m) => {
return [x/w+cx/w, y/h+cy/h, 0]
}
canvas.onmousemove = e => {
var img = c.getImageData(0, 0, w, h)
for(var x = 0; x<w; x++) {
for(var y = 0; y<h; y++) {
let value = formula(x, y, e.x, e.y)
let offset = (yw + x)4
img.data[offset] = value[0]255
img.data[offset + 1] = value[1]255
img.data[offset + 2] = value[2]*255
img.data[offset + 3] = 255
}
}
c.putImageData(img, 0, 0)
}
canvas.onmousemove({x: 456, y: 123})
<canvas width="600" height="175" id="canvas"/>Необходимо реализовать функцию formula для получения "интересного" изображения, дополнительными аргументами выступают координаты мыши
Язык - любой, но желательно js, из-за возможности онлайн визуализации.
PS: рекурсивные методы мне менее интересны, особенно если рекурсия не хвостовая, так какпортировать это на glsl будет сложно если не невозможно.
P.P.S. для привлечения более широкой аудитории мной был выбран cpu и код цикла по картинке я написал для него, однако если Вам угодно, мне больше импонирует webgl, по этому ниже сниппет, где цикл по всем пикселям делает видеокарта, когда я рисую один треугольник, закрывающий весь экран, а функция formula - это фрагментный шейдер :)
let gl = canvas.getContext('webgl');
gl.bindBuffer(gl.ARRAY_BUFFER, gl.createBuffer());
gl.bufferData(gl.ARRAY_BUFFER, new Float32Array([-1, 3, -1, -1, 3, -1]), gl.STATIC_DRAW);
let pid = gl.createProgram();
shader('vertex', gl.VERTEX_SHADER);
shader('fragment', gl.FRAGMENT_SHADER);
gl.linkProgram(pid);
gl.useProgram(pid);
let coords = gl.getAttribLocation(pid, "coords");
gl.vertexAttribPointer(coords, 2, gl.FLOAT, false, 0, 0);
gl.enableVertexAttribArray(coords);
let mouse = gl.getUniformLocation(pid, 'mouse');
let resolution = gl.getUniformLocation(pid, 'resolution');
gl.uniform2f(resolution, gl.drawingBufferWidth, gl.drawingBufferHeight);
let changeCenter = e => {
e = e.touches ? e.touches[0] : e;
gl.uniform2f(mouse, e.pageX - canvas.offsetLeft, e.pageY - canvas.offsetTop);
draw();
}
window.addEventListener('mousemove', changeCenter);
window.addEventListener('touchmove', changeCenter);
draw();
function draw() {
gl.viewport(0, 0, gl.drawingBufferWidth, gl.drawingBufferHeight);
gl.clearColor(0, 0, 0, 0);
gl.drawArrays(gl.TRIANGLES, 0, 3);
}
function shader(src, type) {
let sid = gl.createShader(type);
gl.shaderSource(sid, document.querySelector(script[type="glsl/${src}"]).textContent);
gl.compileShader(sid);
var message = gl.getShaderInfoLog(sid);
gl.attachShader(pid, sid);
if (message.length > 0) {
console.log(src.split('\n').map(function (str, i) {
return ("" + (1 + i)).padStart(4, "0") + ": " + str
}).join('\n'));
throw message;
}
}
<canvas width="600" height="175" id="canvas"/>
<script type="glsl/vertex">
attribute vec2 coords;
void main(void) {
gl_Position = vec4(coords.xy, 0.0, 1.0);
}
</script>
<script type="glsl/fragment">
precision highp float;
uniform vec2 mouse;
uniform vec2 resolution;
void main(void) {
vec2 m = mouse/resolution;
vec2 p = gl_FragCoord.xy/resolution - 0.5;
gl_FragColor = vec4(p, m);
}
</script>